CSAPP Lab1. Datalab

---

Datalab是第二章信息表示法的实验，主要涉及各种数据类型表示方法的应用。

这个lab需要按照要求用严格的代码规范完成。lab附带评分的程序。

1. bitXor

手写按位异或，只允许用&和~（按位取反）。

异或就是位不相等的时候才是0，也就是他们既不都是1，也不都是0.

都不是1，就是~(x&y)。都不是0，就是~(~x & ~y)

int bitXor(int x, int y) {
  return ~(x&y) & ~(~x&~y) ;
}

2. tmin

求最小的二进制补码。最小的补码就是符号位是1，其他全是0，这样就是$2^{31}-0$了。

int tmin(void) {
  return 1<<31;
}

3. isTmax

给一个数，问是不是最大的二进制补码。

对int来说，二进制补码的最大值当然是符号位是0其他全是1，也就是$2^{位数-1}$。

题目只允许使用：! ~ & ^ | +

由于不允许使用循环结构，自然不能一位一位的用|或者&去试。这时候异或^和取反~就成了我们最有用的工具。

考虑返回1的情况，如011,01111,0111111，再考虑返回0的情况，如0110,11110，我们发现最大补码的特点是第一位是0，其他位都是1. 要用到异或，这时候应该用可以用的加法+来使得异或可以发挥用处。

由于最大补码只有第一位是0，所以+1后一定变成如1000，其他任意情况都不满足这一性质。1000和他本身0111是相反的。于是就写成 ~x==(x+1) 。但题目不允许用==，考虑到a^a==0， 于是可以改成：!(~x^(x+1))

但这里有个例外要写特判。-1（1111）+1以后为0，也满足我们的判断条件。所以要特判把-1排除掉。

怎么排除-1呢？-1+1当然==0了。注意到这里允许用!运算符，!x可以用来检测x是否为0. 于是用两个!即可排除-1（x+1=0）的情况。

return !(~x ^ (x+1)) & !!(x+1);

4. allOddBits

给一个数，判断是否他的二进制偶数位都是1. 判断的范围是int范围。

既然范围是$2^{32}$，那只需要设a=10101010101010101010101010101010（32位），然后判断a&x是否等于a就行了。

这里等于还是用异或来判断。将a转换成十进制输入程序：2863311530。

int allOddBits(int x) {
  int a = 2863311530;
  return !((x&a)^a);
}

5. negate

给一个数，输出他的相反数，当然不能用-。

考虑到补码编码，是用除了最高位的值减掉只看最高位表示的值，1可表示为0001，-1可表示为1111. 于是容易看出-1 = ~1 + 1。 推广一下，得到-a = ~a + 1。

int negate(int x) {
  return ~x + 1;
}

6. isAsciiDigit

判断给定x是否 0x30<=x<=0x39。

其实就判断是否x-0x30 和 0x39-x 都>=0就行了。

如何判断>=0呢，对补码编码，最高位的那个bit就表示了正（或0）负。于是只要让他&(10000...（即0x80000000，只有第一位是1，或-2147483648，即int表示的最小值）)，就可以取到那一个特定位的值了。这个技巧还是蛮常用的。这里不给用减号，但前面正好写了negate()，当然要用了。

int isAsciiDigit(int x) {
  int a = x+ negate(0x30);
  int b = 0x39 + negate(x);
  int c = -2147483648;
  return !(a&c) & !(b&c);
}

貌似其他博客不是我这样做的，不过我觉得这样做挺简单的。

7. conditional

要求用位运算实现三目运算符一样的效果。

即：if x == 0 then return z else return y

不能用条件分支，那肯定需要用+来连接两个部分，每个部分在不相关的时候用位运算置0.

用位运算怎么置0呢，当然是x & 0 = 0了。那另外那边怎么保持原样呢？

其实刚刚我们就发现，-1的二进制表示是111111...111。于是x & -1 = x。

这里可以用!!x和!x得到对应的1和0，再利用上面的negate()就可以得到-1和0了。

int conditional(int x, int y, int z) {
  return (y&negate(!!x)) + (z&negate(!x));
}

一行解决，貌似比我看到的题解都简单。

8. isLessOrEqual

判断两个数是否小于等于。

上面我们写过判断>=了，把符号交换一下就可以复用了。

int isLessOrEqual(int x, int y) {
  int a = y + negate(x);
  int b = -2147483648;
  return !(a&b);
}

题目没有讲数据范围，如果数据范围大的话可能会爆int（事实上评测下来没有）。如果要写的很完善，可以额外写一个逻辑判断溢出（本不该发生改变的符号产生改变）。

9. logicalNeg

实现!运算符。即if x == 0 then return 1 else return 0

考虑以下事实：

对补码，正数与零的最高位为0，而负数的最高位为1；

在negate（取相反数）操作时，正数和负数的最高位都会变换，而零在操作时最高位不会变换。

于是我们可以对x取相反数，将0和正数区分开来；而0和负数在表示上本质不同，很容易区分他们。

右移时，若最高位为1，则填充的bit为1，否则为0。于是得到技巧：

要得到最高位，可使x>>31，若值为-1（1111...11），则最高位为1；若值为0，则最高位为0。

于是我们可以用 negate(x)| x 来区分。对于正数，其值为1xxxx..xx | 0xxx..xx，对于负数，其值也为0xxx..xx | 1xxx..xx ，结果都为1xx..xx。于是我们右移31位，他们的结果都是-1；对于0，其值始终为0.

这样我们再最后给他+1，就达到为0返回1，其他返回0的效果了。

int logicalNeg(int x) {
  return ( (negate(x)| x) >>31) +1 ;
}

10. howManyBits

求最高的一位有效位是多少。

这题有点奇怪，其实就是暴力位移了以后判断，要优化的话也就走一个倍增，不知道有没有更好的做法。

首先要处理负数，如果是负数就按位取反。原理是决定负数补码表示的值的位是左边数第一个0。例如1101和11101表示的值是一样的。按位取反以后0就变成1，1变成0，就和正数的处理方法一样了。取符号sign为0或1，结合&和|，就很好处理了。

接下来就暴力的倍增，设变量left16 left8 left4 left2 left1 left0，分别表示剩下的x位中是否有1。从16开始，每次进行一下位移，来检测剩下16位中是否有1.如果有，则右移16位，同时记录在变量上；如果没有则不移动。然后再到8,4，...以此类推。

最后把记录的移动的位数加起来，再+1（符号位也要算在内）就行了。

int howManyBits(int x) {
  int left16,left8,left4,left2,left1,left0;
  int sign = x>>31;
  x = (sign & ~x) | (~sign & x);
  left16 = (!!(x>>16))<<4;
  x>>=left16;
  left8 = (!!(x>>8))<<3;
  x>>=left8;
  left4 = (!!(x>>4))<<2;
  x>>=left4;
  left2 = (!!(x>>2))<<1;
  x>>=left2;
  left1 = !!(x>>1);
  x>>=left1;
  left0 = x;
  return left16 + left8 + left4 + left2 + left1 + left0 + 1;
}

11. floutScale2

这题用整数模拟浮点数结构，要求把浮点数*2.

首先题目要求判断是否是NaN，如果是的话就直接return。

32位单精度浮点数由1位符号位s，8位阶码（指数），23位尾数按顺序组成。

对于NaN和无穷，就是exp全是1的情况，按题目要求直接return uf。

下面要考虑两种编码形式。

规格化编码，即exp!=0时，用于编码>1的数。这时候flac的值=1+M（实际表示的尾数），所以不能直接乘2，而应该给阶码exp+1（相当于给指数+1）。

非规格化编码，即exp==0，用于编码<1的数。这时候flac的值就是M，因为编码的是<1的数，所以不能随便加exp。直接对M*2.

unsigned floatScale2(unsigned uf) {
  unsigned s,exp,frac;
  s = (uf>>31)&1;
  exp = (uf&0x7f800000)>>23;
  frac = uf&0x7fffff;
  unsigned ans;
  if(exp == 0xff) return uf;
  if(exp == 0) ans = (s<<31) | (exp<<23) | frac<<1;
  else ans = (s<<31) | ((exp+1)<<23) | frac;
  return ans;
}

12. floatFloat2Int

题意是将给定浮点数表示转换成整数。

转换浮点数到整数的时候要注意到浮点数能表示的范围比int大得多，如果超出范围要按照题意返回0x80000000u。什么时候超出范围？E>=31的时候，int就32位，指数这么大换算到int里肯定超范围了。

剩下的都是规格化表示了。由于int是要舍掉小数精度的，由于尾数部分是23位，而E是阶数，如果E<23的话那尾数部分是不能全部位于小数点左边的，所以要右移(23-E)（不能在小数点左边的部分）舍掉。如果>=23的，就将阶数正常乘上去（左移）即可。

最后再处理下符号，return的时候改一下就行了。另外要注意在操作尾数之前要先把尾数隐含的头部的那个1给他补上。

int floatFloat2Int(unsigned uf) {
  unsigned s,exp,frac;
  s = (uf>>31)&1;
  exp = (uf&0x7f800000)>>23;
  frac = uf&0x7fffff;
  int ans;
  int E = exp-127;

  if(E<0) return 0;
  if(E>=31) return 0x80000000u;
  ans = frac | 1<<23;
  if(E<23) ans>>=(23-E);
  else ans<<=(E-23);

  if(s) return -ans;
  else return ans;
}

13. floatPower2

题意：求$2^x$，要用浮点数表示。

这题难点主要在于判断各种范围。

首先浮点数的范围是$2^{-149}\ 到\ 2^{127}$，其中上界是由exp的最大值决定的，下界是由非规格数的最小值决定的。

参考图：

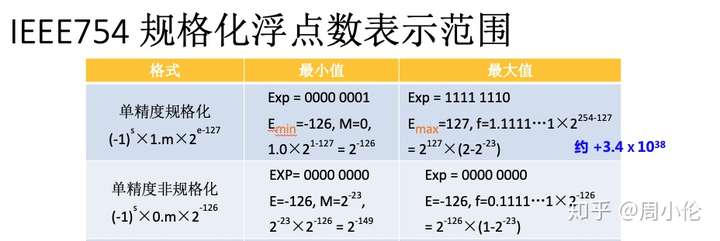
如果超出上界，返回无限（11110000..00），如果超出下界，返回0.

对于x<-126的情况，要拿非规格化数来表示；其他情况就拿规格化数来表示就好了。

构建规格化数，只需要改exp部分即可。非规格数就改flac部分。

unsigned floatPower2(int x) {
    if(x<-149) return 0;
    if(x>127) return 0xff<<23;
    if(x<-126) return 1<<(x+149);
    return (x+127)<<23;
}

13个小任务做完，顺利拿到满分。

补充

输入一个浮点数（以字符串形式输入），输出其用IEEE754格式的二进制表示，按int输出（不考虑非规格数）：

int my_int_float(){
    char s[50]; int sign;
    scanf("%s",s);

    sign = (s[0]=='-');     //求符号位
    int len = strlen(s);
    if(!sign){   // 统一正负形式
        for(int i = len;i>0;i--){
            s[i] = s[i-1];
        }
    }

    int dot;    //找小数点
    for(int i = 1;i<=len;i++)
        if(s[i]=='.') dot = i;

    int upper_num = 0;
    int index = 0, tmp = 1;
    for(int i = dot-1;i>=1;i--){ //处理小数点左边
        int num = s[i] - '0';
        upper_num += num * tmp;
        tmp*=10;
        index++;
    }

    int lower_num = 0;
    int lower_len = len - dot; //处理小数点右边
    index = 0; tmp = 1; int lower_tot = 0;
    for(int i = len;i>dot;i--){
        int num = s[i] - '0';
        lower_tot += num * tmp;
        tmp*=10;
        index++;
    }
    int target = 1;
    for(int i = 1;i<=lower_len;i++) target*=10;
    lower_num = target/lower_tot;

    tmp = 1; index = 0;
    while(tmp<=upper_num){  //拼接两边，求阶码
        index++;
        tmp*=2;
    }
    int exp = index -1 + 127;

    lower_num >>=1; //根据小数点右边位的性质，舍掉一位
    tmp = 1; index = 0;
    int right_len;  //求小数点右边二进制表示的长度
    while(tmp<=lower_num){
        index++;
        tmp*=2;
    }
    right_len = index;

    int right_num = 0;
    for(int i = 1;i<=right_len;i++){    //求小数点右边的二进制表示（小数格式）
        right_num |= (((lower_num&(1<<(right_len-i)))>0)<<(i-1));
    }

    int M_pre = upper_num;  //求尾数（不考虑尾0）
    M_pre <<= right_len;
    M_pre |= right_num;

    tmp = 1; index = 0;
    int M;
    while(tmp<=M_pre){  //为尾数补0，减去默认的1
        index++;
        tmp*=2;
    }
    M = (M_pre<<(23-index)) - (1<<22);
    M<<=1;

    int ans = 0;
    ans |= (sign<<31); //拼装符号位
    ans |= M;   //拼接尾数
    ans |= (exp<<23); //拼接阶码
    return ans;
}