快乐树0x01:AVL树的java实现
1. AVL树
2. 节点
节点定义
public class AVLTree<T extends Comparable<T>>{
//用java自带的泛型,实现Comparable接口做比较
Node<T> root;//跟节点
class Node<T extends Comparable<T>>{
T value;
Node<T> left;
Node<T> right;
int height; //节点的高度
public Node(T key, Node<T> left, Node<T> right){
this.value = key;
this.left = left;
this.right = right;
this.height = 0;
}
}
}取height函数
3. 旋转

LL的旋转
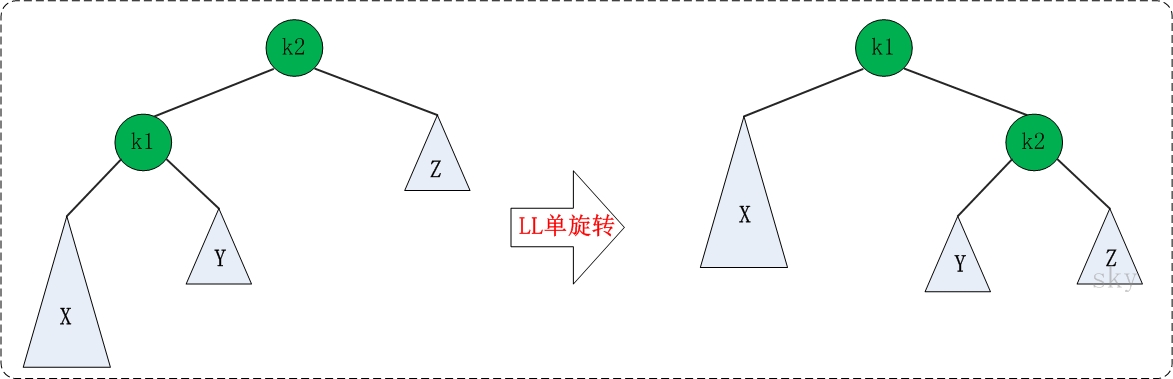
RR的旋转
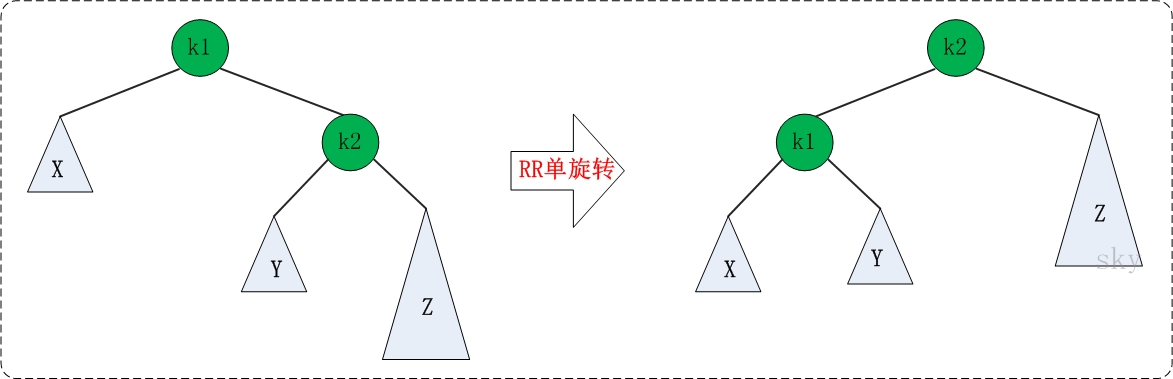
LR的旋转

RL的旋转

4. 插入
5. 删除
最后更新于